[March 2: Read the follow-up article, Comparing paths with the pros in Google Earth]

[March 9: Read the follow-up article, Three trajectory models of the Chelyabinsk meteoroid compared]

[April 5: Help scientists to more accurately calculate the trajectory. Visit www.russianmeteor2013.org to contribute videos or help with the analysis.]

Like many others, I was absolutely astounded by the meteor strike over Chelyabinsk when I woke on Friday morning. One silver lining to our self-surveilling society is that an event of this magnitude is certain to get caught on the myriad of always-on dash- and webcams. I for one could not get enough of the videos.

Might it be possible to use this viral footage with Google Earth to have an initial go at mapping the meteorite’s trajectory? I was pondering this question some 2,500km away from Chelyabinsk when I chanced upon this video:

That place is easy to find — it’s Revolution Square at the absolute center of Chelyabinsk, looking almost directly south. It is also easy to measure — the distance between the two central light poles is 32 meters, as per a quick measurement in Google Earth, while the five lanes of traffic going right to left (west to east) measure 19 meters. From this it is easy to estimate the height of the light poles to be around 12 meters — an estimate corroborated by numerous panoramas in Google Earth showing people next to these lamp posts, giving us added data points.

Using all this information, I was able to do some image analysis in Photoshop on the lengths and angles of the shadows as the meteor streaked across the sky. Here’s an animated gif showing the result of that:

The ensuing grade-school mathematics (SOHCAHTOA!) resulted in three lines of sight at three instants a few seconds apart. (For the sake of the record, I roughly calculated them to be towards 122 degrees at an inclination of 33 degrees at 9:20:28.7, towards 187 degrees at an inclination of 40 degrees at 9:20:32.2, and towards 222 degrees at an inclination of 32 degrees at 9:20:33.4. These times are the video’s own timeline, though they appear to correlate closely with the timelines of other videos.)

This allowed me to draw an inclined plane in Google Earth that should include the meteor’s path, though it does not allow me to know the distance of the meteor from central Chelyabinsk, nor its speed.

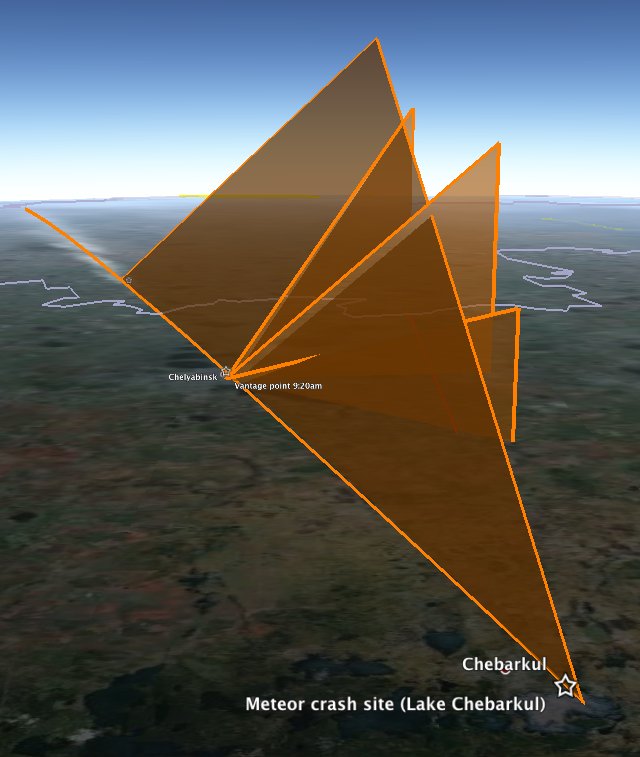
However, we have more clues. We know a fragment of the meteor landed in Lake Chebarkul, roughly 70km WSW of Chelyabinsk. Gratifyingly, the inclined plane generated from the above video intersects with the crash site. Also useful was the estimate by the Russian Academy of Sciences that the meteorite hit the Earth’s atmosphere at around 50,000 km/h, shattering at an altitude of 30-50km. If that was the rough speed of the meteor as it burned up in the video, then the 4.7 seconds between the first and last shadow measurements would have seen it travel 65 km. Fitting a 65km line between these two lines of sight allows us to draw a straight line path for the meteor towards the crash site, with the first measured time yielding a height of 29km, which is the moment the meteor first brightened enough to give a clear shadow.

Download the visualizations for this as a KMZ file to open in Google Earth. Do play with the opacity slider of the overlay to check the alignments yourself — it’s most of the fun.

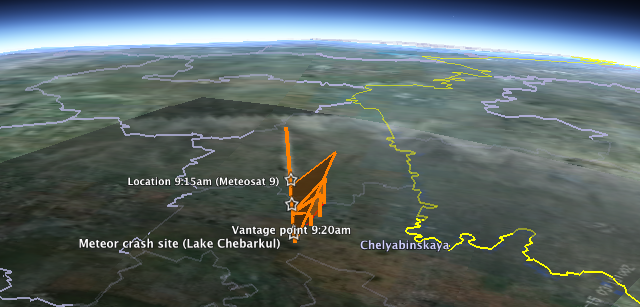
How does this data square with the Meteosat 9 image that has being doing the rounds? At first glance, not well: Overlaying the image in Google Earth and aligning the border with Kazakhstan shows a 240km contrail that appears to end some 75km to the ENE of Chelyabinsk, even though the path when traced on the ground also leads directly to Lake Chebarkul.

At first, I thought the image might have been taken 5 minutes earlier, before the meteor streaked straight across Chelyabinsk proper, because the image’s metadata gives us a time of 3:15:00Z, or UTC, which is 6 hours behind Chelyabinsk time. But no meteor is going to take 5 minutes to traverse 75km, so we’ll just have to live with the time discrepancy. Webcams are not atomic clocks.

Much more interesting is the fact that if you look at the position of Meteosat 9, which is in a geostationary orbit, you see that Chelyabinsk is near the horizon of its view of Earth. This leads to extreme foreshortening in the snapshot of the meteor’s contrail:

(Notice the outline of the Sea of Azov in the foreground. Here is another version showing the thermal impact (source).)

The version used in the overlay is an enhanced view of this image, taken from the same angle. (The blacked-out upper right-hand corner of the overlay is behind the horizon as seen from Meteosat 9.). If you simulate this view of Chelyabinsk in Google Earth, you see that in fact, the contrail aligns quite nicely over Chelyabinsk considering that it would be 30km high and at such an extreme angle over the horizon. So the 4.7 seconds of maximal brightness (with contrail) do get to happen just south of Chelyabinsk proper, as per the above video, and without contradiction by Meteosat 9.

I feel this post would not be complete without some big caveats: I am not a trained scientist; I don’t know if meteors travel through the atmosphere in straight lines or at constant speeds (I assume they don’t, but that it doesn’t matter for back-of-the-envelope type calculations). Still, it is satisfying to know that with judicious use of Google Earth, YouTube and Photoshop you can get quite far in the meteor simulation game. I can’t wait to see what the professionals come up with.

UPDATE 2013-02-16: Via SebastienP in the comments comes another triangulation, comparing the calculated path from the KMZ file with the view from another dash cam. It holds up pretty well!

(Source)

UPDATE 2013-02-17: In this comment, some smart calculations by Sean Mac are confirmed by a video he’s found showing the contrail crossing almost exactly above the southern suburb of Yemanzhelinsk. I found the exact vantage point of the video he references in Google Earth by connecting this Panoramio photo to this view in the video.

This suggests the meteor’s trajectory towards Earth was higher and steeper along the inclined plane of sight derived from the central Chelyabinsk vantage point than the initial calculation suggested. That’s not surprising, as that calculation was based on an initial estimate of the velocity by the Russian Academy of Sciences, which now appears to have been on the low side.

I’ve now added a second path for the meteor in Google Earth, together with the location of the vantage point in Yemanzhelinsk, in this KMZ file. Open it as a complement to the first KMZ file to see what I would consider to be an upper bound (green) for the trajectory along the same inclined plane, with a new likeliest path (red).

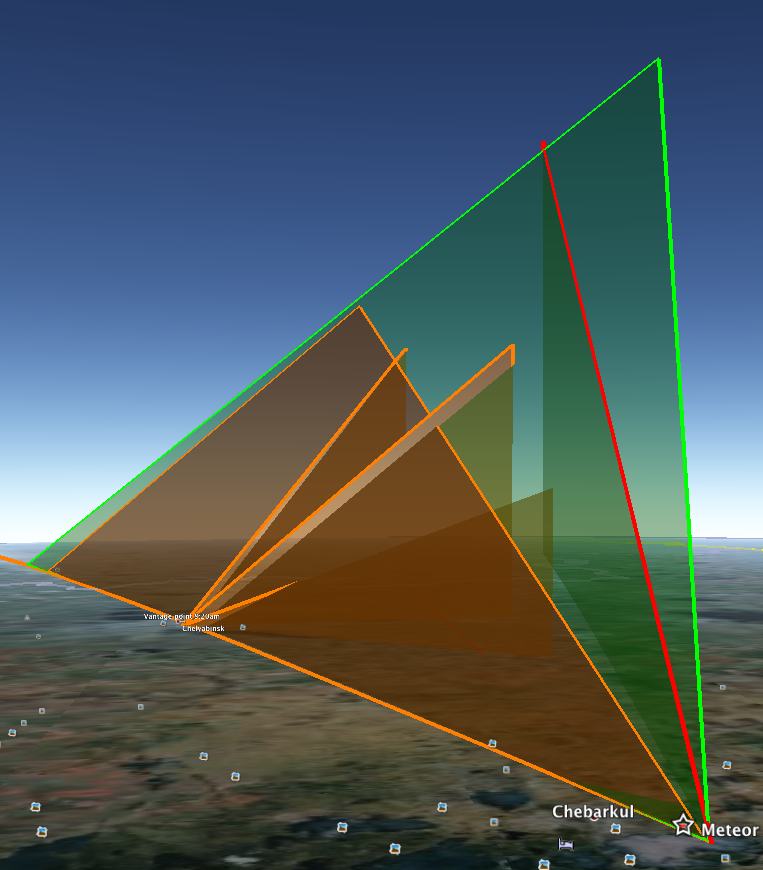
“Looking up” in Google Earth from the vantage point in Yemanzhelinsk (I can because I have a 3D mouse from 3DConnexion), I get a very similar angle of view of the contrail when framed by the NNW axis of the buildings on that square.

A further video showing the perspective from the town of Korkino further north (included in the new KMZ file) shows that the meteor passed a little to the south of there, allowing for a pretty accurate triangulation. (Thanks to Robin Whittle and liilliil in the comments for the heads up.)

UPDATE 2013-02-22: OK, so this is kind of special: An astrophysics paper has just been submitted to ArXiv.org that models the orbit of the Chelyabinsk meteor, referencing this blog post as a starting point: A preliminary reconstruction of the orbit of the Chelyabinsk Meteoroid by Jorge I. Zuluagaa and Ignacio Ferrin. Details are here, and here comes the resulting animation:

[March 2: Read the follow-up article, Comparing paths with the pros in Google Earth]

[March 9: Read the follow-up article, Three trajectory models of the Chelyabinsk meteoroid compared]

[April 5: Help scientists to more accurately calculate the trajectory. Visit www.russianmeteor2013.org to contribute videos or help with the analysis.]